Basic use

Setting up a simulation

A typical input file contains the following:

Listing 2 /../../tests/jobs/couple_NiCrSi/couple_NiCrSi-input.txt
# Thermodynamic and mobility databases
thermo_db = schuster2000
mob_db    = du2001

# System constituents
independent    = Si, Cr                  # independent constituents
dependent      = Ni                      # dependent constituent

# System conditions
phase     = fcc                          # phase
TC        = 1200                         # temperature (Celsius)

# Simulation conditions
th        = 10                           # total time (h)
num_out   = 11                           # number of saved time steps, optional

# Domain geometry
geometry  = planar                       # optional

# Initial space grid
zmin      = 0                            # position of left-hand domain border (m), optional
zmax      = 5e-4                         # position of right-hand domain border (m)
nz        = 60                           # number of space steps, optional
grid      = linear                       # grid type, optional

# Initial atom fraction profile
x_profile = step 0.5                     # profile type and options
x_left    = Si: 0, Cr: 0.3               # independent constituents on left-hand side
x_right   = Si: 0.1, Cr: 0               # independent constituents on right-hand side

# Boundary conditions
JBC_left  = Si: 0, Cr: 0, Ni: 0          # flux of atom constituents on left boundary, optional
JBC_right = Si: 0, Cr: 0, Ni: 0          # flux of atom constituents on right boundary, optional

Blank lines and code located after the comment character # are ignored when the file is parsed. Parameters are to be entered with the following syntax: key = value, with any number of spaces around the = sign. Some keys have an accepted alias (shorter name), as shown below.

Element symbols are case-insensitive — for instance, fe is a valid symbol for iron.

Some of the parameters are optional. When an optional parameter is not present in the input file, a default value is assigned. “Factory” default values are defined in the package installation but can be overridden by user-defined values (see Default parameters).

Thermodynamic and mobility databases

  • thermo_db: name of the thermodynamic database to be used in the calculation.

  • mob_db: name of the mobility database to be used in the calculation.

These names must be associated with database files in user_data.toml.

System constituents

  • independent: name independent constituents, with the following syntax:
    element1, element2, .... Alias: inds.

  • dependent: name of the dependent constituent. This is typically the alloy base element.|br| Alias: dep.

System conditions

  • phase: name of the phase.

  • TC: temperature in Celsius.

Simulation conditions

  • th: simulation time in h.

  • num_out: number of saved time steps, optional (factory default: 2). A simulation often requires a large number of time steps; only the number of steps specified by num_out are saved to file, and accessible after the simulation is done.

Note

The initial and last step are always saved, and these two steps are included in num_out. Therefore num_out must be greater than or equal to 2. For instance, if the simulation time is 2 h and one wants to access the results that correspond to 1 h of simulation, one may use
num_out = 3. This will save results at 0, 1 and 2 h of simulation (saved_times = [0, 1, 2]).

Domain geometry

Noda solves the diffusion problem along one space coordinate, in either of three geometric configurations:

  • planar : a slab of given thickness in one direction and translational symmetry in the two other directions, described in Cartesian coordinates.

  • cylindrical : a cylinder with translational and rotational symmetry with respect to its axis, described in cylindrical coordinates.

  • spherical : a sphere with rotational symmetry with respect to its center, described in spherical coordinates.

The geometry parameter takes either argument (‘planar’, ‘cylindrical’ or ‘spherical’). It is optional (factory default: ‘planar’).

Note

The rotational symmetry in the cylindrical and spherical geometries has implications regarding the choice of the domain boundary positions and boundary conditions (see Initial space grid).

Initial space grid

  • zmin: position of left-hand domain boundary in m, optional (system default: 0).

  • zmax: position of right-hand domain boundary in m.

  • nz: number of space steps, optional (factory default: 51).

  • grid: optional (factory default: ‘linear’). Can be either a standard grid type or a file name:

    • ‘linear’: linear grid from zmin to zmax with size nz.

    • ‘geo’: geometric grid from zmin to zmax with size nz and common ratio q:
      \(\Delta z_{i+1} = q \Delta z_{i}\). The common ratio is indicated as an additional parameter, for example q = 1.02. It is optional (factory default: 1.02).

    • filename: read grid positions from file in the current job folder. The file can be in any format readable by the Numpy genfromtxt method. zmin, zmax and nz are inferred from the grid file, and must not be included in the input file.

Note

As shown in Diffusion, grid positions correspond to the edges of the volumes (nodes, noted z). Fluxes are evaluated on nodes. Composition and related variables (concentrations, atom fractions, chemical potentials, molar volumes, …) are evaluated in the center of the volumes, noted zm. For instance, with grid = linear, nz = 4 and zmax = 3 will produce
z = [0, 1, 2, 3] and zm = [0.5, 1.5, 2.5].

Note

At the moment, Noda only includes an explicit (forward Euler) time integration scheme, which is conditionnally stable. The minimum time step is based on the smallest space step (see Time step). Using a geometric grid with a large common ratio will produce locally small space steps and therefore require a large number of time steps.

Note

In the cylindrical and spherical geometries:

  • The space coordinate is named \(z\), instead of the usual \(\rho\) or \(r\), to favor compatibility across the three geometries.

  • The simulation domain is represented by positive radial coordinates, and the left-hand domain border is closest to the centre of symmetry. Therefore the following is enforced: \(0 \leq z_\mathrm{min} < z_\mathrm{max}\).

  • If zmin = 0, the left-hand domain boundary is at the axis (or center) of symmetry. In this case, it is recommended to use a 0-flux boundary condition at this boundary.

  • It is possible to represent a hollow cylinder (or sphere) by giving a strictly positive value to zmin.

Initial atom fraction profile

  • x_profile: can be either a standard profile type or a file name:

    • ‘step’ followed by a float argument: heaviside profile with step at zstep.
      If the argument is > 0.1, it is interpreted as a fraction of the domain length
      \(\rightarrow\) zstep = zmin + arg * (zmax - zmin).
      If the argument is < 0.1, it is interpreted as zstep in m.
      The atom fractions on the left and right sides of the step are read from the x_left and x_right parameters (both required).

    • ‘smooth step’ followed by a float: same with an error function instead of heaviside.

    • ‘flat’: flat profile. The atom fractions are read from the x_left parameter (required).

    • filename: read values from file in the current job folder. The file can be in any format readable by the Numpy genfromtxt method. It must have the independent constituent profiles arranged by columns, with the constituent names on the first line. The size of the columns must match that of zm (i.e., nz - 1). x_left and x_right must not be used.

  • x_left: name and atom fractions of each independent constituent on the left-hand side, with the following syntax: element1: value, element2: value, ....

  • x_right: same on the right-hand side.

Boundary conditions

Noda supports Neumann (fixed flux) and Dirichlet (fixed composition) boundary conditions. For each of the left and right boundary, the user can specify a composition (atom fractions of the independent constituents) or fluxes (of all atom constituents). If no condition is given, a zero flux condition is applied.

  • JBC_left: flux of atom constituents on left boundary, with the following syntax:
    element1: value, element2: value, ...
    The value is in SI units (mol/m2/s). It can also be an expression of time (noted t) with basic Python operators, which will be evaluated with eval, ex: (3*t + 2)**(1/2). If JBC_left is used, values must be given for all atom constituents.

  • JBC_right: same on right boundary.

  • xBC_left: atom fractions of independent constituents on left boundary, with the following syntax: element1: value, element2: value, ...
    It can also be an expression of time (noted t) with basic Python operators. If xBC_left is used, values must be given for all independent constituents.

  • xBC_right: same on right boundary.

Note

Internally, Dirichlet boundary conditions are implemented by setting fluxes of the independent constituants in the lattice reference frame. By default, a flux of the dependent constituent is set so that the sum of the volumetric fluxes at the boundary is 0:

\[J_n^\mathrm{lat} = -\frac{1}{V_n}\sum_{i=1}^{n - 1} J_i^\mathrm{lat}V_i,\]

where the \(V_i\) are the partial molar volumes. The volume of the simulation domain is conserved. The quantity of atom matter (in mol) may change due to differences in the partial molar volumes.

Optional parameters

The user may also specify:

  • A partial molar volume database, with key volume_db. The factory default is standard.

  • A vacancy formation energy database, with key vacancy_db. The factory default is standard.

Like the other optional parameters, the factory default values can be overridden by user-specified default values (see Default parameters).

Running a diffusion simulation

A new simulation is created using the simu.NewSimulation class:

from noda import simu
foo = simu.NewSimulation('couple_NiCrSi')

This supposes that an input file named couple_NiCrSi-input.txt is present in the working directory. When the simulation is created, some information is logged:

  • Part of it (with the INFO level) is printed to screen and saved to the log file (here couple_NiCrSi.nod): this indicates what default choices are made for all parameters not present in the input file, and gives general information as to how thermodynamics and mobility functions are generated.

  • Another part (with the DATA level) is only saved to the log file: this contains data that will be used when loading the simulation.

The simulation is then run with the simu.Simulation.run() method:

foo.run()

Once the calculation is done, Noda logs the run time (screen and log file) and the results (to the log file only).

Accessing and plotting simulation results

Simulation results may be accessed either directly after a new simulation is run (see above), or by loading the log file from a simulation run in a previous session. In the latter case, the simulation is created using the simu.ReadSimulation class:

foo = simu.ReadSimulation('couple_NiCrSi')

This supposes that a log file named couple_NiCrSi.nod is present in the working directory.

The simulation results are stored at a number of time steps. The steps and the associated simulation times (in h) can be accessed using the saved_steps and saved_times attributes of the simulation object:

>>> foo.saved_steps
array([  0,  47,  94, 141, 188, 235, 282, 329, 376, 423, 470])
>>> foo.saved_times
array([ 0.,  1.,  2.,  3.,  4.,  5.,  6.,  7.,  8.,  9., 10.])

Note

The unit of saved_times is hours. Here, there are 11 saved steps including the initial step (\(t=0\)), and the simulated time is 10 h. However, the time step is not exactly a rational number multiplied by 3600. It follows that the saved times are not necessarily integer numbers of hours.

Other useful attributes are:

>>> foo.th       # time (h)
10.0
>>> foo.ts       # time (s)
36000.0
>>> foo.dt       # time step (s)
76.59574468085107
>>> foo.nt       # number of time steps
471
>>> foo.num_out  # number of saved time steps
11

Accessing results

The results are accessed using the results.SimulationResults.result() method. The simulation time one would like to access is specified with either of two keyword arguments:

  • step_index, which is the index of the required step in saved_steps. step_index must be an integer between 0 and the number of saved steps.

  • th, a time in h. In this case the simulation time accessed will be the closest to the specified value.

The results are also accessible as a dictionary of results objects. The dictionary is called results and uses time steps as keys.

To wrap up, these are three ways to access the results after 4 h of simulation:

bar = foo.result(step_index=4)
bar = foo.result(th=4)
bar = foo.results[188]

Both step_index and th are optional arguments of results.SimulationResults.result(). If no argument is given, the method uses the default step_index = -1, which is an alias for the last time step, i.e., foo.result() returns the results at the last time step. Similarly, foo.results[-1] returns the results at the last time step.

The results objects (instances of results.UnitResult) have attributes which store the simulation variables as Numpy arrays (or dictionaries of Numpy arrays). Commonly used attributes are:

  • z : Node positions (m).

  • zm : Midpoint positions (m).

  • c : Concentrations (mol/m3).

  • y : Metal site fractions.

  • x : Metal atom fractions.

  • Vm : Average molar volume of metal (m3/mol).

  • mu : Chemical potentials (J/mol).

  • Jlat : Fluxes in lattice-fixed frame (mol m-2 s-1).

  • v : Velocity field of lattice relative to laboratory frame (m/s).

  • deformation : Relative length variation.

Composition variables such as x or c are stored as dictionaries of 1D arrays, with the relevant constituents as keys. The relevant constituents are vacancies and all atom constituents, except for atom fractions x which only apply to atom constituents:

>>> bar.x.keys()
dict_keys(['Cr', 'Si', 'Ni'])
>>> bar.c.keys()
dict_keys(['Va', 'Cr', 'Si', 'Ni'])
>>> bar.Jlat.keys()
dict_keys(['Va', 'Cr', 'Si', 'Ni'])

Composition variables are also accessible as 2D arrays of shape (nc, nz - 1) where nc is the number of constituents. These 2D arrays are named with the suffix ‘_arr’, for example x_arr.

Plotting results

Profiles of the simulated variables can be plotted using the results.UnitResult.plot() method. The variable is specified with the optional argument varname, which defaults to x:

  • bar.plot(varname='Jlat') will plot fluxes in the lattice reference frame.

  • bar.plot() will plot atom fractions.

It is also possible to call plot directly from the simulation object; in this case, the time step is specified with the optional arguments th or step_index, which defaults to the last time step:

  • foo.plot(varname='v', th=3) will plot the lattice velocity after 3 h.

  • foo.plot(th=3) will plot atom fractions after 3 h.

  • foo.plot(varname='mu') will plot chemical potentials at the last time step.

  • foo.plot() will plot atom fractions at the last time step.

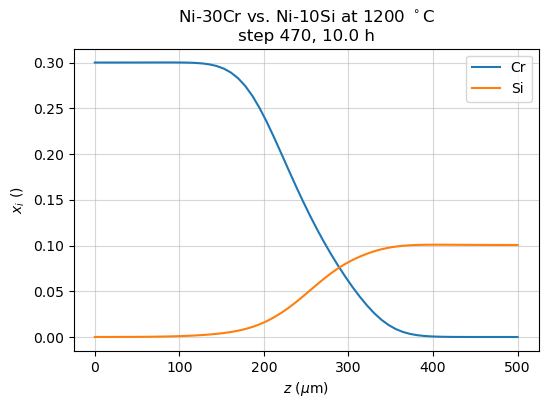
_images/couple_NiCrSi.png

The results.UnitResult.plot() method returns matplotlib figure and axis objects. This allows modifying the graph settings after it is generated, for example:

fig, ax = foo.plot()
ax.set_title('Custom title')

The results.SimulationResults.interactive_plot() method allows accessing time steps dynamically on a plot using a slider. Again the variable to be plotted is specified with the optional argument varname, which defaults to x, and a shortcut is accessible from the simulation object:

  • foo.interactive_plot(varname='mu') will plot chemical potentials.

  • foo.interactive_plot() will plot atom fractions.

Note

Interactive plots require an interactive graphics backend. If you are using Spyder, you will need to set the graphics backend to ‘Automatic’ rather than ‘Inline’ (see Tools/Preferences/IPython console/Graphics/Graphics backend).

Accessing thermodynamic and diffusion properties

Noda contains methods to compute the thermodynamic and diffusion properties of a system, at given compositions. This can be done from a simulation object (an instance of the simu.NewSimulation class, see above), or by creating a system object with the alloy_system.AlloySystem class:

from Noda import alloy_system
foo = alloy_system.AlloySystem('NiCrSi')

The input file for alloy_system.AlloySystem instances only requires the following parameters:

Listing 3 /../../tests/jobs/properties_NiCrSi/NiCrSi-input.txt
thermo_db = schuster2000
mob_db    = du2001

independent    = Si, Cr
dependent      = Ni 

phase     = fcc_a1
TC        = 1200

The following example illustrates how properties are computed:

Listing 4 /../../tests/jobs/properties_NiCrSi/run.py
import numpy as np

from noda import simu

foo = simu.AlloySystem('NiCrSi')

# The independent constituents are Cr and Si, in alphabetical order:
assert foo.inds == ['Cr', 'Si']

# Make atom fraction array
# The required shape is (n_inds, n_points), where n_inds is the number of
# independent constituents, and n_points the number of compositions of
# interest. Here n_inds = 2. The independent constituents must be entered in
# the order used by foo.inds (alphabetical).
x_Cr = np.array([0.1, 0.2, 0.3])
x_Si = np.array([0.1, 0.1, 0.01])
x = np.vstack((x_Cr, x_Si))

# Compute Gibbs free energy, shape = (n_points,)
G = foo.G_fun(x)

# Compute chemical potentials, shape = (n ind. constituents, n_points)
MU = foo.MU_fun(x)

# Compute tracer diffusion coefficients, shape = (n ind. constituents, n_points)
DT = foo.DT_fun(x)


#%% Validation

ref = np.genfromtxt('NiCrSi-ref.txt', skip_header=1, delimiter=',').T
x_ref = ref[:2]
G_ref = ref[2:3]
MU_ref = ref[3:6]
DT_ref = ref[6:9]

assert np.allclose(x, x_ref)
assert np.allclose(G, G_ref)
assert np.allclose(MU, MU_ref)
assert np.allclose(DT, DT_ref)

The methods shown here are also accessible from simu.NewSimulation instances.

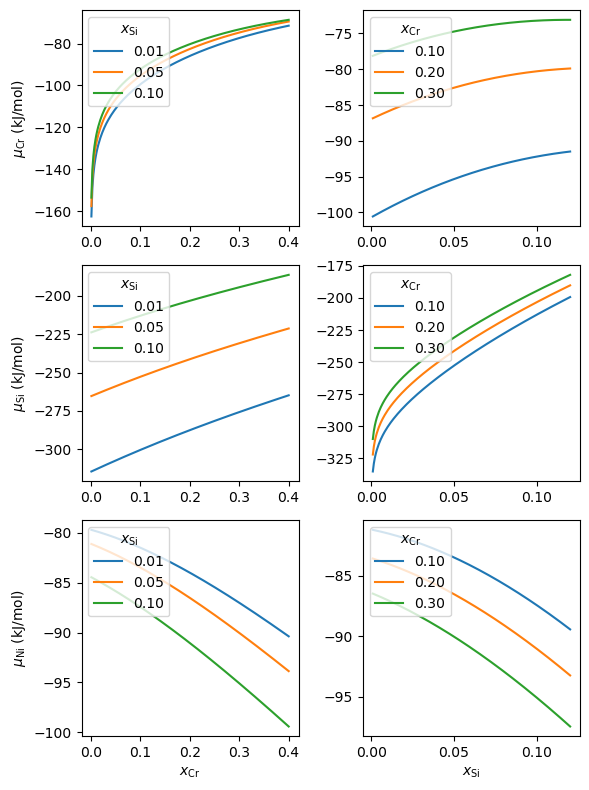
Thermodynamic and diffusion properties are obtained as ndarrays and may be plotted using standard matplotlib commands:

Listing 5 /../../tests/jobs/properties_NiCrSi/plot.py
import numpy as np
import matplotlib.pyplot as plt

from noda import simu

s = simu.AlloySystem('NiCrSi')

#%% Gibbs free energy

fig, ax = plt.subplots()
for val in [0.01, 0.05, 0.1]:
    x0 = np.linspace(1e-3, 0.4)
    x1 = np.ones(x0.size)*val
    x = np.vstack((x0, x1))
    G = s.G_fun(x)
    ax.plot(x0, G/1000, label=f'{val:.2f}')
ax.set_xlabel(r'$x_\mathrm{Cr}$')
ax.set_ylabel('$G$ (kJ/mol)')
ax.legend(title=r'$x_\mathrm{Si}$', loc='upper left')

#%% Chemical potentials

fig, axes = plt.subplots(3, 2, figsize=(6, 8), tight_layout=True)

for i in range(3):
    
    A = s.comps[i + 1]
    ax1 = axes[i, 0]
    ax2 = axes[i, 1]

    targets = [0.01, 0.05, 0.1]
    x0 = np.linspace(1e-3, 0.4, num=200)
    
    for j, val in enumerate(targets):
        x1 = np.ones(x0.size)*val
        x = np.vstack((x0, x1))
        MU = s.MU_fun(x)[i]/1000
        ax1.plot(x0, MU, label=f'{val:.2f}')
    
    ax1.set_ylabel(rf'$\mu_\mathrm{{{A}}}$ (kJ/mol)')
    ax1.legend(title=r'$x_\mathrm{Si}$', loc='upper left')
    
    targets = [0.1, 0.2, 0.3]
    x1 = np.linspace(1e-3, 0.12, num=200)
    
    for j, val in enumerate(targets):
        x0 = np.ones(x1.size)*val
        x = np.vstack((x0, x1))
        MU = s.MU_fun(x)[i]/1000
        ax2.plot(x1, MU, label=f'{val:.2f}')
    
    ax2.legend(title=r'$x_\mathrm{Cr}$', loc='upper left')

ax1.set_xlabel(r'$x_\mathrm{Cr}$')
ax2.set_xlabel(r'$x_\mathrm{Si}$')

# plt.savefig('chemical_potentials_NiCrSi.png', bbox_inches="tight", dpi=100)

#%% Tracer diffusion coefficients

fig, axes = plt.subplots(3, 2, figsize=(6, 8), tight_layout=True)

for i in range(3):
    
    A = s.comps[i + 1]
    ax1 = axes[i, 0]
    ax2 = axes[i, 1]

    targets = [0.01, 0.05, 0.1]
    x0 = np.linspace(1e-3, 0.4, num=200)
    
    for j, val in enumerate(targets):
        x1 = np.ones(x0.size)*val
        x = np.vstack((x0, x1))
        DT = s.DT_fun(x)[i]
        ax1.plot(x0, np.log10(DT), label=f'{val:.2f}')
    
    ax1.set_ylabel(rf'$\log_{{{10}}}\ D_\mathrm{{{A}}}^*$ (m$^2$/s)')
    ax1.legend(title=r'$x_\mathrm{Si}$', loc='upper left')
    
    targets = [0.1, 0.2, 0.3]
    x1 = np.linspace(1e-3, 0.12, num=200)
    
    for j, val in enumerate(targets):
        x0 = np.ones(x1.size)*val
        x = np.vstack((x0, x1))
        DT = s.DT_fun(x)[i]
        ax2.plot(x1, np.log10(DT), label=f'{val:.2f}')
    
    ax2.legend(title=r'$x_\mathrm{Cr}$', loc='upper left')

ax1.set_xlabel(r'$x_\mathrm{Cr}$')
ax2.set_xlabel(r'$x_\mathrm{Si}$')
_images/chemical_potentials_NiCrSi.png

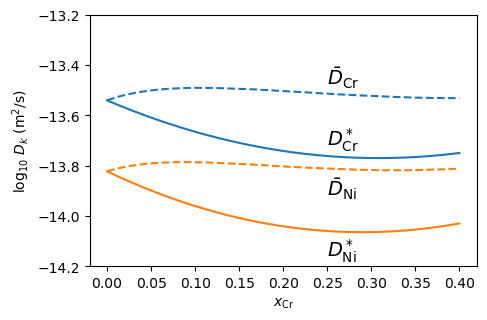
The following example shows how to plot tracer diffusion coefficients and intrinsic diffusion coefficients in a binary system. It reproduces Figure 3 in [Gheno_2022]:

Listing 6 /../../tests/jobs/properties_NiCr/plot.py
import numpy as np
import matplotlib.pyplot as plt

from noda import simu
from noda.constants import R

s = simu.AlloySystem('NiCr')

#%% Prepare data

comps = [k for k in s.comps if k != 'Va']

x0 = np.linspace(1e-9, 0.4, num=200)
x = x0[np.newaxis]

DT = s.DT_fun(x)
MU = s.MU_fun(x)
phi = -(1 - x0)/(R*s.TK)*np.gradient(MU[1], x0)
DI = DT*phi

#%% Plot

colors = ['tab:blue', 'tab:orange']

fig, ax = plt.subplots(figsize=(5,5/1.5))
for i, k in enumerate(comps):
    ax.plot(x0, np.log10(DT[i]), c=colors[i], label=k)
    ax.plot(x0, np.log10(DI[i]), '--', c=colors[i])

ax.set_xlabel(r'$x_\mathrm{Cr}$')
ax.set_ylabel(r'$\log_{10}\ D_k$ (m$^2$/s)')
ax.set_ylim(-14.2, -13.2)
fs = 14
xpos = 0.25
ax.annotate(r'$\bar{D}_\mathrm{Ni}$', (xpos, -13.92), fontsize=fs)
ax.annotate(r'$D^*_\mathrm{Ni}$', (xpos, -14.16), fontsize=fs)
ax.annotate(r'$\bar{D}_\mathrm{Cr}$', (xpos, -13.48), fontsize=fs)
ax.annotate(r'$D^*_\mathrm{Cr}$', (xpos, -13.72), fontsize=fs)
# plt.savefig('diffusivities_NiCr.png', bbox_inches="tight", dpi=100)
_images/diffusivities_NiCr.png

Working with model systems

Users can easily explore the effects of thermodynamic and diffusion properties on the shape of concentration profiles by creating their own database files. The examples below shows how the known solution to the diffusion problem is recovered when the system properties follow a particular set of constraints.

Let us consider a single-phase binary system AB, where the average molar volume is composition-independent. In 1D, the diffusion problem may be written in the following form:

\[ \begin{align}\begin{aligned}\frac{1}{V_\mathrm{m}}\frac{\partial x_B}{\partial t} = -\frac{\partial \tilde{J}_B}{\partial z}\\\tilde{J}_B = -\frac{\tilde{D}}{V_\mathrm{m}}\frac{\partial x_B}{\partial z}\end{aligned}\end{align} \]

This problem has analytical solutions when the interdiffusion coefficient is constant — in this case:

\[\frac{\partial x_B}{\partial t} = \tilde{D}\frac{\partial^2 x_B}{\partial z^2}\]

If A and B are both substitutional constituents of a disordered phase, the interdiffusion coefficient is given by Darken’s formula:

\[\tilde{D} = (x_A D_B^* + x_B D_A^*)\phi\]

where \(\phi\) is the thermodynamic factor:

\[\phi = \frac{x_B}{RT}\frac{\partial \mu_B}{\partial x_B}\]

The simplest way for \(\tilde{D}\) to be composition-independent is that the system follows the following set of conditions:

  • AB is an ideal solution: \(\mu_B = \mu_B^0 + RT\ln{x_B}\), which yields \(\frac{\partial \mu_B}{\partial x_B} = \frac{RT}{x_B}\) and \(\phi = 1\);

  • A and B have equal diffusivities: \(D_A^* = D_B^*\);

  • The diffusivities are composition-independent: \(D_B^* \neq f(x_B)\).

This yields \(\tilde{D} = D_B^*\).

These conditions are fullfilled for the model AB system provided in the test base, with databases named “thermo_bin_ideal” and “mob_bin_ideal”.

A number of diffusion problems involving a binary system with composition-independent molar volume and diffusivity have analytical solutions. Some typical initial distributions and boundary conditions are illustrated below.

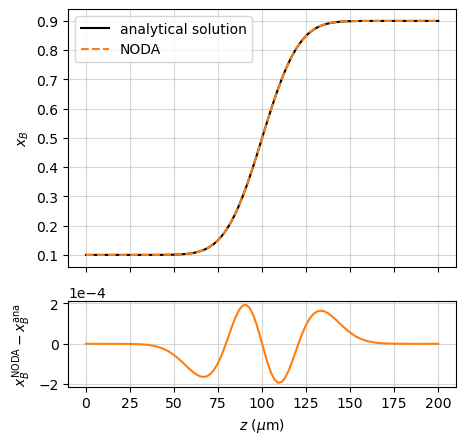
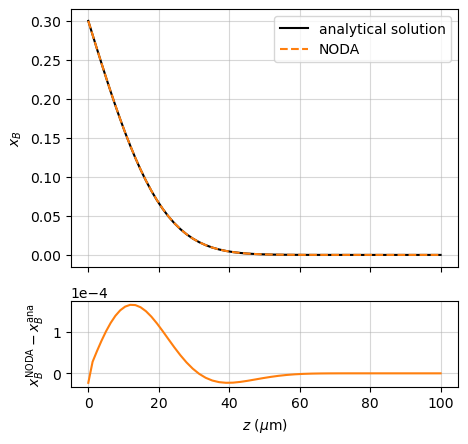
Diffusion couple (planar geometry)

In the case of an infinitely-thick planar diffusion couple:

\[\begin{split}&t = 0,\ z < z_\mathrm{step},\ x_B = x_B^\mathrm{left}\\ &t = 0,\ z > z_\mathrm{step},\ x_B = x_B^\mathrm{right}\\ &t > 0,\ \left.\frac{\partial x_B}{\partial z}\right|_{z\rightarrow -\infty} = \left.\frac{\partial x_B}{\partial z}\right|_{z\rightarrow +\infty} = 0,\end{split}\]

the analytical solution to the diffusion problem is ([Crank_1975], p. 14):

\[\frac{x_B(z, t) - x_B^\mathrm{right}}{x_B^\mathrm{left} - x_B^\mathrm{right}} = \frac{1}{2} \mathrm{erfc}\left(\frac{z - z_\mathrm{step}}{2\sqrt{\tilde{D}t}}\right)\]

This is compared with the Noda simulation in the example named “couple_AB”:

Listing 7 /../../tests/jobs/couple_AB/couple_AB-input.txt
# Thermodynamic and mobility databases
thermo_db = thermo_bin_ideal
mob_db    = mob_bin_ideal

# System constituents
independent    = B
dependent      = A

# System conditions
phase     = fcc
TC        = 1000

# Simulation conditions
th        = 1

# Initial space grid
zmin      = 0
zmax      = 2e-4
nz        = 100

# Initial atom fraction profile
x_profile = step 0.5
x_left    = B: 0.1
x_right   = B: 0.9

# Boundary conditions
JBC_left   = A: 0, B: 0
JBC_right  = A: 0, B: 0

# Space discretization
stencil = H
Listing 8 /../../tests/jobs/couple_AB/run.py
import numpy as np
from scipy.special import erfc
import matplotlib.pyplot as plt

from noda import simu

s = simu.NewSimulation('couple_AB')
s.run()

#%% Comparison with analytical solution

x_left = s.x_init['B'][0]
x_right = s.x_init['B'][-1]

x_any = np.array([[0.5]])
D = s.DT_fun(x_any)[0]

r = s.results[-1]
zmid = (r.z[-1] + r.z[0])/2
x_ana = x_right + (x_left - x_right)*0.5*erfc((r.z - zmid)/np.sqrt(4*D*s.ts))

fig, (ax1, ax2) = plt.subplots(nrows=2, ncols=1,
                               figsize=(5, 5),
                               gridspec_kw={'height_ratios': [3, 1]})
ax1.plot(r.z*1e6, x_ana, 'k', label='analytical solution')
ax1.plot(r.z*1e6, r.x['B'], '--', c='tab:orange', label='Noda')
ax1.set_ylabel('$x_B$')
ax1.set_xticklabels([])
ax1.legend()
ax1.grid(visible=True)

ax2.plot(r.z*1e6, r.x['B'] - x_ana, c='C1')
ax2.set_xlabel(r'$z$ ($\mu$m)')
ax2.set_ylabel(r'$x_B^\mathrm{Noda} - x_B^\mathrm{ana}$')
ax2.grid(visible=True)

# plt.savefig('couple_AB.png', bbox_inches="tight", dpi=100)

#%% Validation

assert np.allclose(r.x['B'], x_ana, atol=2e-4)
_images/couple_AB.png

Constant surface concentration (planar geometry)

In the case of a semi-infinite planar solid initially at a uniform concentration \(x_B^\mathrm{bulk}\), with its left-hand surface maintained at a constant concentration \(x_B^\mathrm{surf}\):

\[\begin{split}&t = 0,\ x_B = x_B^\mathrm{bulk}\\ &t > 0,\ z = 0,\ x_B = x_B^\mathrm{surf},\end{split}\]

the solution reads ([Crank_1975], p. 32):

\[\frac{x_B(z, t) - x_B^\mathrm{bulk}}{x_B^\mathrm{surf} - x_B^\mathrm{bulk}} = \mathrm{erfc}\left(\frac{z}{2\sqrt{\tilde{D}t}}\right)\]

This is compared with the Noda simulation in the example named “source_AB”, which illustrates the use of a geometric grid, well suited to the Dirichlet boundary condition:

Listing 9 /../../tests/jobs/source_AB/source_AB-input.txt
# Thermodynamic and mobility databases
thermo_db = thermo_bin_ideal
mob_db    = mob_bin_ideal

# System constituents
independent    = B
dependent      = A

# System conditions
phase     = fcc
TC        = 1000

# Simulation conditions
th        = 1

# Initial space grid
grid      = geo
q         = 1.02
zmin      = 0
zmax      = 1e-4
nz        = 50

# Initial atom fraction profile
x_profile = flat
x_left    = B: 1e-4

# Boundary conditions
xBC_left = B: 0.3
xBC_right = B: 1e-4

# Space discretization
stencil = G
Listing 10 /../../tests/jobs/source_AB/run.py
import numpy as np
from scipy.special import erfc
import matplotlib.pyplot as plt

from noda import simu

s = simu.NewSimulation('source_AB')
s.run()

#%% Comparison with analytical solution

x_bulk = s.x_init['B'][0]
x_surf = s.BC['c_left'](0).x.mid[0]

x_any = np.array([[0.5]])
D = s.DT_fun(x_any)[0]

r = s.results[-1]
x_ana = x_bulk + (x_surf - x_bulk)*erfc(r.z/np.sqrt(4*D*s.ts))

fig, (ax1, ax2) = plt.subplots(nrows=2, ncols=1,
                               figsize=(5, 5),
                               gridspec_kw={'height_ratios': [3, 1]})
ax1.plot(r.z*1e6, x_ana, 'k', label='analytical solution')
ax1.plot(r.z*1e6, r.x['B'], '--', c='tab:orange', label='Noda')
ax1.set_ylabel('$x_B$')
ax1.set_xticklabels([])
ax1.legend()
ax1.grid(visible=True)

ax2.plot(r.z*1e6, r.x['B'] - x_ana, c='C1')
ax2.set_xlabel(r'$z$ ($\mu$m)')
ax2.set_ylabel(r'$x_B^\mathrm{Noda} - x_B^\mathrm{ana}$')
ax2.grid(visible=True)

# plt.savefig('source_AB.png', bbox_inches="tight", dpi=100)

#%% Validation

assert np.allclose(r.x['B'], x_ana, atol=2e-4)
_images/source_AB.png

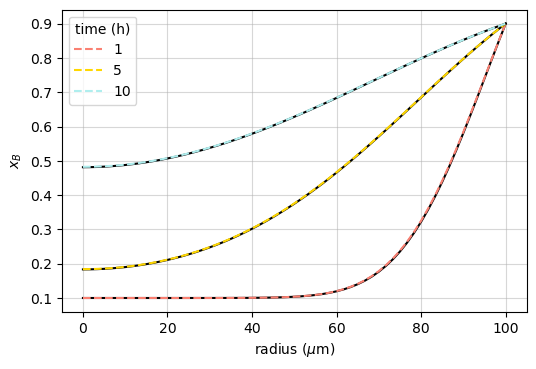
Constant surface concentration (spherical geometry)

If a sphere of radius \(R\) is initially at a uniform concentration \(x_B^\mathrm{bulk}\), and its surface is maintained at a constant concentration \(x_B^\mathrm{surf}\), the concentration at distance \(r\) from the center is ([Crank_1975], p. 91):

\[\frac{x_B(r, t) - x_B^\mathrm{bulk}}{x_B^\mathrm{surf} - x_B^\mathrm{bulk}} = 1 + \frac{2R}{\pi r} \sum_{n=1}^{\infty} \frac{(-1)^n}{n} \sin{\left(\frac{n\pi r}{R}\right)} \exp\left(\frac{-Dn^2\pi^2t}{R^2}\right)\]

This is compared with the Noda simulation after different diffusion times in the example named “sphere_AB”:

Listing 11 /../../tests/jobs/sphere_AB/sphere_AB-input.txt
# Thermodynamic and mobility databases
thermo_db        = thermo_bin_ideal
mob_db           = mob_bin_ideal

# System constituents
independent      = B
dependent        = A

# System conditions
phase            = fcc
TC               = 1000

# Simulation conditions
th               = 10
nt_multiplier    = 1.2
num_out          = 11

# Initial space grid
geometry         = spherical
zmin             = 0
zmax             = 1e-4
nz               = 61

# Initial atom fraction profile
x_profile = flat
x_left    = B: 0.1

# Boundary conditions
JBC_left = B: 0, A: 0
xBC_right = B: 0.9
Listing 12 /../../tests/jobs/sphere_AB/run.py
import numpy as np
import matplotlib.pyplot as plt

from noda import simu

def analytical_solution(r, R, D, ts, x_bulk, x_surf, N=100):
    f = 1 + 2*sum(((-1)**n)
                  * np.divide(R*np.sin(n*np.pi*r/R), np.pi*n*r,
                              out=np.ones(r.size), where=(r!=0))
                  * np.exp(-D*n**2*np.pi**2*ts/R**2)
                  for n in range(1, N))
    x = x_bulk + (x_surf - x_bulk)*f
    return x

s = simu.NewSimulation('sphere_AB')
s.run()

#%% Comparison with analytical solution

x_bulk = s.x_init['B'][0]
x_surf = s.BC['c_right'](0).x.mid[0]
R = s.zmax
r = s.z_init

x_any = np.array([[0.5]])
D = s.DT_fun(x_any)[0]

th_targets = [1, 5, 10]
colors = ['salmon', 'gold', 'paleturquoise']

fig, ax = plt.subplots()
for th_target, c in zip(th_targets, colors):
    th = s.saved_times[np.argmin(abs(th_target - s.saved_times))]
    res = s.result(th=th)
    x_ana = analytical_solution(r, R, D, th*3600, x_bulk, x_surf)
    ax.plot(r*1e6, x_ana, 'k')
    ax.plot(r*1e6, res.x['B'], '--', c=c, label=f"{th:.0f}")
ax.set_xlabel(r'radius ($\mu$m)')
ax.set_ylabel('$x_B$')
ax.legend(title='time (h)')
ax.grid(visible=True)
fig.set_dpi(200)

# plt.savefig('sphere_AB.png', bbox_inches="tight", dpi=100)

#%% Validation

assert np.allclose(res.x['B'], x_ana, atol=2e-3)
_images/sphere_AB.png

References

[Crank_1975] (1,2,3)

J. Crank, The mathematics of diffusion, 2nd ed., Oxford University Press, Oxford, 1975